Progress has been made in the study of ultrafast motion of Weil quasiparticles controlled by lasers

In recent years, the theoretical and experimental research on topological quantum states and topological quantum materials has become a hot topic in the field of condensed matter physics. As a new concept of matter classification, topological order, like symmetry, is a fundamental concept in condensed matter physics. A deep understanding of topology is related to the basic problems in condensed matter physics, such as the basic electronic structure of quantum phases, quantum phase transitions and excitation of many immobilized elements in quantum phases. In topological materials, the coupling between many degrees of freedom, such as electrons, phonons and spin, plays a decisive role in understanding and regulating material properties. Light excitation can be used to distinguish between different interactions and manipulate the state of matter, and information about the material's basic physical properties, structural phase transitions, and new quantum states can then be obtained. At present, the relationship between macroscopic behavior of topological materials driven by light field and their microscopic atomic structure and electronic properties has become a research goal.

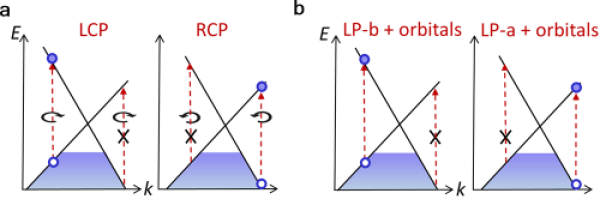
The photoelectric response behavior of topological materials is closely related to its microscopic electronic structure. For topological semi-metals, the carrier excitation near the band intersection is highly sensitive to the wave function characteristics of the system. The study of nonlinear optical phenomena in topological semi-metals can help us to better understand the physical properties of the excited states of the system, and it is expected that these effects can be used in the manufacture of optical devices and the design of solar cells, providing potential practical applications in the future. For example, in a Weyl semi-metal, absorbing a photon of circularly polarized light will cause the spin to flip, and in order to meet the conservation of angular momentum, the electron excitation on both sides of the Weyl cone will be asymmetrically distributed along the direction of the circularly polarized light propagation, which is called the chiral selection rule (Figure 1).

The theoretical study of nonlinear optical phenomena of topological materials usually adopts the method of combining the calculation of material ground state properties and symmetry analysis. However, this method has some defects: it lacks the real-time dynamic information of excited carriers in momentum space and real space, and it cannot establish a direct comparison with the time-resolved experimental detection method. The coupling between electron-phonons and photon-phonons cannot be considered. And this is crucial for certain phase transitions to occur. In addition, this theoretical analysis based on perturbation theory cannot deal with the physical processes under the strong light field. The time-dependent density functional molecular dynamics (TDDFT-MD) simulation based on first principles can solve the above problems.

Recently, under the guidance of researcher Meng Sheng, postdoctoral researcher Guan Mengxue and doctoral student Wang En of the SF10 Group of the State Key Laboratory of Surface Physics of the Institute of Physics of the Chinese Academy of Sciences/Beijing National Research Center for Concentrated Matter Physics, in collaboration with Professor Sun Jiatao of the Beijing Institute of Technology, they used the self-developed excited state dynamics simulation software TDAP. The response characteristics of quastiparticle excitation to ultrafast laser in the second kind of Weyl semi-metal WTe2 are investigated.

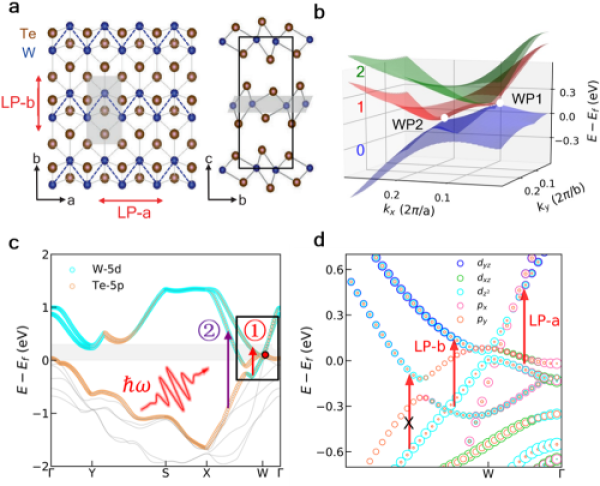
It has been shown that the selective excitation of carriers near the Weyl point is determined by atomic orbital symmetry and transition selection rule, which is different from the usual spin selection rule for chiral excitation, and its excitation path can be controlled by changing the polarization direction of linearly polarized light and photon energy (FIG. 2).

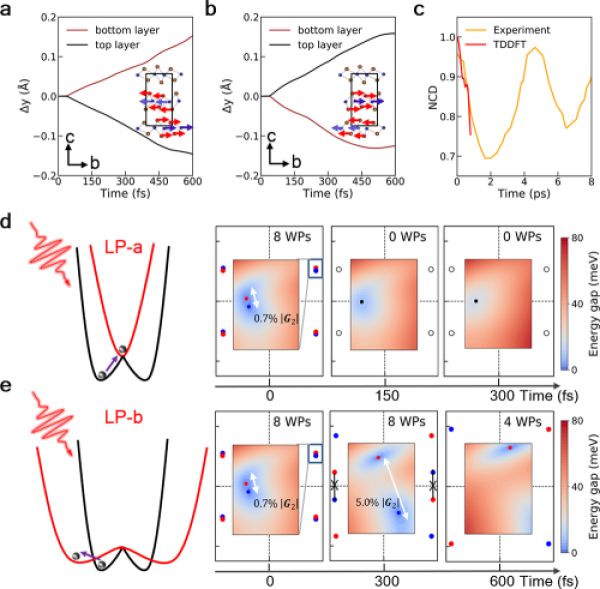
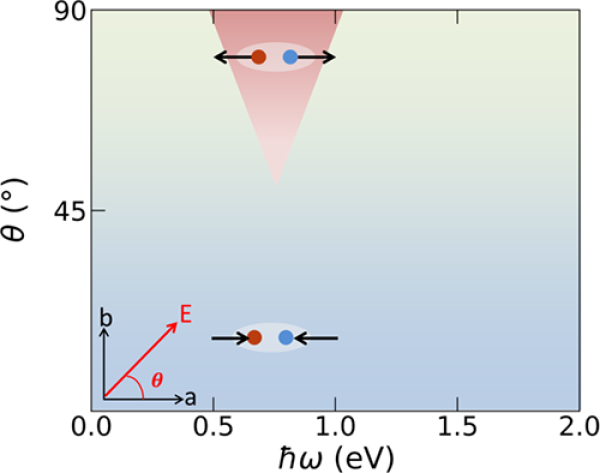
The asymmetric excitation of carriers induces photocurrents in different directions in real space, which affects the direction and symmetry of the interlayer slip of the system. Since the topological properties of WTe2, such as the number of Weyl points and the degree of separation in the momentum space, are highly dependent on the symmetry of the system (Figure 3), the asymmetric excitation of carriers will bring about different behavior of Weyl quastiparticles in the momentum space and corresponding changes in the topological properties of the system. Thus, the study provides a clear phase diagram for phototopological phase transitions (Figure 4).

The results show that the chirality of carrier excitation near Weyl point should be paid attention to, and the atomic orbital properties of wave function should be analyzed. The effects of the two are similar but the mechanism is obviously different, which provides a theoretical basis for explaining the singularity of Weyl points. In addition, the computational method adopted in this study can deeply understand the complex interactions and dynamical behaviors at the atomic and electronic levels in a super-fast time scale, reveal their microphysical mechanisms, and is expected to be a powerful tool for future research on nonlinear optical phenomena in topological materials.

The results are in the journal Nature Communications. The research work is supported by the National Key Research and Development Plan, the National Natural Science Foundation and the Strategic Pilot Project (Category B) of the Chinese Academy of Sciences.

FIG.1.a. The chirality selection rule for Weyl points with positive chirality sign (χ=+1) under circularly polarized light; Selective excitation due to atomic orbital symmetry at the Weyl point of b. χ=+1 in on-line polarized light

FIG. 2. Atomic structure diagram of a, Td-WTe2; b. Band structure near the Fermi surface; (c) Band structure and relative contributions of atomic orbitals distributed along high symmetric lines in the Brillouin region, arrows (1) and (2) represent excitation near or far from Weyl points, respectively; d. Amplification of band structure along the Gamma-X direction

FIG.3.a-b: The relative interlayer movement of linearly polarized light polarization direction along the A-axis and B-axis of the crystal, and the corresponding movement mode is illustrated; C. Comparison between theoretical simulation and experimental observation; d-e: Symmetry evolution of the system and the position, number and degree of separation of the two closest Weyl points in the kz=0 plane

FIG. 4. Phototopological phase transition in Td-WTe2 for linearly polarized light photon energy (?) ω) and polarization direction (θ) dependent phase diagram